Kekongruenan dan Kesebangunan Kelas 9 MATEMATIKA

 

Kekongruenan dan Kesebangunan Kelas 9

Kekongruenan dan Kesebangunan - Kekongruenan dan Kesebangunan adalah salah satu bagian dari ilmu geometri yang agak mirip. Kekongruenan adalah dua buah bangun yang memiliki bentuk dan ukuran yang sama dilambangkan dengan simbol ≅. Sedangkan kesebangunan adalah dua buah bangun yang memiliki bentuk yang sama akan tetapi ukuran berbeda dilambangkan dengan simbol ≈.

Kekongruenan

Dua bangun yang mempunyai bentuk dan ukuran yang sama dinamakan kongruen. Jika kita hubungkan dengan materi sebelumnya yaitu transformasi, maka kita bisa katakan bahwa semua bangun datar yang  ditransformasi dengan cara refleksi, translasi dan rotasi memiliki sifat kekongruenan. 

Syarat Dua Bangun Datar Kongruen

Dua bangun segi banyak (poligon) dikatakan kongruen jika memenuhi dua syarat, yaitu: 

(i) sisi-sisi yang bersesuaian sama panjang, dan 

(ii) sudut-sudut yang bersesuaian sama besar

Sudut-sudut yang bersesuaian: 

 ∠A dan ∠J → m∠A = m∠J 

 ∠B dan ∠K → m∠B = m∠K 

 ∠C dan ∠L → m∠C = m∠L 

 ∠D dan ∠M → m∠D = m∠M 

Sisi-sisi yang bersesuaian: 

 AB dan JK → AB = JK 

 BC dan KL → BC = KL 

 CD dan LM → CD = LM 

 DA dan MJ → DA = MJ 

Jika bangun ABCD dan JKLM memenuhi kedua syarat tersebut, maka bangun ABCD dan JKLM kongruen, dinotasikan dengan ABCD ≅ JKLM. Jika bangun ABCD dan JKLM tidak memenuhi kedua syarat tersebut maka bangun ABCD dan JKLM tidak kongruen, dinotasikan dengan ABCD ≅ JKLM. 

Contoh Soal :

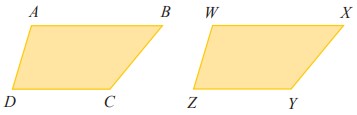
1. Segi empat ABCD dan WXYZ pada gambar di bawah kongruen. Manakah sisi-sisi dan sudut-sudut yang bersesuaian?

Alternatif Penyelesaian:

2. Manakah persegi di bawah yang kongruen? Jelaskan!

Alternatif Penyelesaian: 

Dua bangun dikatakan kongruen jika memenuhi dua syarat, yaitu: 

(i) sudut-sudut yang bersesuaian sama besar Setiap persegi mempunyai empat sudut siku-siku, sehingga sudut-sudut yang bersesuaian pada persegi (a), (b) dan (c) besarnya pasti sama.

(ii) sisi-sisi yang bersesuaian sama panjang 

Persegi (a) dan persegi (b) 

Panjang setiap sisi persegi (a) adalah 8 cm. Panjang setiap sisi persegi (b) adalah 9 cm. Jadi, sisi-sisi yang bersesuaian persegi (a) dan (b) tidak sama panjang. 

Persegi (b) dan persegi (c) 

Panjang setiap sisi persegi (b) adalah 9 cm. Panjang setiap sisi persegi (c) adalah 8 cm. Jadi, sisi-sisi yang bersesuaian persegi (b) dan (c) tidak sama panjang. 

Persegi (a) dan persegi (c) 

Panjang setiap sisi persegi (a) adalah 8 cm. Panjang setiap sisi persegi (c) adalah 8 cm. 

Jadi, sisi-sisi yang bersesuaian persegi (a) dan (c) sama panjang. Berdasarkan (i) dan (ii) di atas, maka persegi yang kongruen adalah persegi (a) dan (c). 

3. Perhatikan gambar trapesium ABCD dan PQRS yang kongruen di bawah ini.

a. Jika panjang sisi AB = 40 cm, BC = 21 cm, RS = 16 cm, dan PS = 15 cm, tentukan panjang sisi AD, DC, PQ, dan QR. 

b. Jika besar ∠A = 60o , ∠B = 40o . Berapakah besar ∠R dan ∠S? (selanjutnya, besar ∠A ditulis dengan m∠A, seperti yang sudah kamu kenal di kelas 7 dan 8) 

Alternatif Penyelesaian: 

Diketahui: bangun ABCD ≅ PQRS, berarti 

• sisi-sisi yang bersesuaian sama panjang 
• sudut-sudut yang bersesuaian sama besar 

a. Untuk menentukan panjang sisi AD, DC, PQ, dan QR, tentukan terlebih dulu sisisisi yang bersesuaian yaitu:

(mengapa bukan AB = SR? Jelaskan) 

Dengan demikian, jika AB = 40 cm, BC = 21 cm, RS = 16 cm, dan PS = 15 cm maka: 

AD = PS = 15 cm 

DC = SR = 16 cm 

QR = BC = 21 cm 

PQ = AB = 40 cm

b. Untuk menentukan m∠R dan m∠S, tentukan terlebih dulu sudut-sudut yang bersesuaian yaitu:

Dengan demikian, jika m∠A = 60o , m∠B = 40o maka: 

m∠P = m∠A = 60o dan 

m∠Q = m∠B = 40o 

m∠R + m∠Q = 180o 

m∠R = 180o – m∠Q 

m∠R = 180o – 40o 

m∠R = 140o 

m∠S = 180o – m∠P 

m∠S = 180o – 60o 

m∠S = 120o Jadi 

m∠R = 140o dan m∠S = 120o .

Syarat Dua Segitiga KongruenDua bangun yang mempunyai bentuk dan ukuran yang sama dinamakan kongruen. Dua segitiga dikatakan kongruen jika hanya jika memenuhi syarat berikut ini: 

(i) sisi-sisi yang bersesuaian sama panjang 

(ii) sudut-sudut yang bersesuaian sama besar.

Sisi-sisi yang bersesuaian:

AB dan DE → AB = DE

BC dan EF → BC = EF

CA dan FD → CA = FD

Sudut-sudut yang bersesuaian:

∠A dan ∠D → m∠A = m∠D

∠B dan ∠E → m∠B = m∠E

∠C dan ∠F → m∠C = m∠F

atau dengan kata lain 

Jika ∆ABC dan ∆DEF memenuhi syarat tersebut, maka ∆ABC dan ∆DEF kongruen, dinotasikan dengan ∆ABC ≅ ∆DEF. 

Jika ∆ABC dan ∆DEF tidak memenuhi syarat tersebut maka maka ∆ABC dan ∆DEF tidak kongruen, dinotasikan dengan ∆ABC ≇ ∆DEF.

Untuk menguji apakah dua segitiga kongruen atau tidak , tidak perlu menguji semua pasangan sisi dan sudut yang bersesuaian. Dua segitiga dikatakan kongruen jika memenuhi salah satu kondisi berikut ini: 

1. Ketiga pasangan sisi yang bersesuaian sama panjang. Biasa disebut dengan kriteria sisi – sisi – sisi.
2. Dua pasang sisi yang bersesuaian sama panjang dan sudut yang diapitnya sama besar. Biasa disebut dengan kriteria sisi – sudut – sisi.
3. Dua pasang sudut yang bersesuaian sama besar dan sisi yang menghubungkan kedua sudut tersebut sama panjang. Biasa disebut dengan kriteria sudut – sisi – sudut.
4. Dua pasang sudut yang bersesuaian sama besar dan sepasang sisi yang bersesuaian sama panjang. Biasa disebut dengan kriteria sudut – sudut – sisi.
5. Khusus untuk segitiga siku-siku, sisi miring dan satu sisi siku yang bersesuaian sama panjang.

Contoh Soal

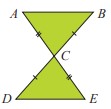
1. Perhatikan gambar di bawah.

Buktikan bahwa ∆ABC ≅ ∆EDC.

Berdasarkan gambar di atas diperoleh bahwa: 

AC = EC (diketahui ada tanda sama panjang) 

m∠ACB = m∠ECD (karena saling bertolak belakang) 

BC = DC (diketahui ada tanda sama panjang) 

Jadi, ∆ABC ≅ ∆EDC (berdasarkan kriteria sisi – sudut – sisi).

2. Perhatikan gambar di bawah.

Buktikan bahwa ∆PQS ≅ ∆RQS.

Alternatif Penyelesaian: Berdasarkan gambar di atas diperoleh bahwa: 

PQ = RQ (diketahui ada tanda sama panjang) 

PS = RS (diketahui ada tanda sama panjang) 

QS pada ∆PQS sama dengan QS pada ∆RQS (QS berimpit) 

Jadi, ∆PQS ≅ ∆RQS (berdasarkan kriteria sisi – sisi – sisi).

Kesebangunan

Bangun datar dikatakan sebangun jika memiliki bentuk yang sama walaupun ukurannya berbeda. Kesebangunan sebenarnya bisa kita katakan hasi dari transformasi dilatasi.

Syarat Kesebangunan Bangun Datar

Dua bangun datar yang mempunyai bentuk yang sama disebut sebangun. Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan. 

Dengan kata lain dua bangun dikatakan sebangun jika memenuhi syarat:

(i) perbandingan panjang sisi yang bersesuaian senilai

(ii) sudut yang bersesuaian besarnya sama

m∠A = m∠E

m∠B = m∠F

m∠C = m∠G

m∠D = m∠H

Jika bangun ABCD dan EFGH memenuhi kedua syarat tersebut, maka bangun ABCD dan EFGH sebangun, dinotasikan dengan ABCD ∼ EFGH. 

Jika bangun ABCD dan EFGH tidak memenuhi kedua syarat tersebut maka bangun ABCD dan EFGH tidak sebangun, dinotasikan dengan ABCD ≁ EFGH. 

Contoh Soal

Perhatikan gambar di bawah ini. 

Bangun ABCD dan EFGH sebangun. 

Tentukan nilai x, y dan z!

Alternatif Penyelesaian: 

Bangun ABCD dan EFGH sebangun berarti sudut-sudut yang bersesuaian sama besar dan perbandingan sisi-sisi yang bersesuaian senilai, yaitu: 

m∠E = m∠A, m∠F = m∠B, m∠G = m∠C, m∠H = m∠D, 

Bangun ABCD dan EFGH sebangun dengan sudut-sudut yang bersesuaian m∠E = m∠A, m∠F = m∠B, m∠G = m∠C, dan m∠H = m∠D, 

Sehingga,

m∠G = m∠C ⇔ xo = 22,6o 

m∠D = 180o – m∠C ⇔ yo = 180o – xo = 180o – 22,6o = 157,4o (Mengapa?) 

m∠H = m∠D ⇔ zo = yo = 157,4o 

Jadi, nilai adalah xo = 22,6o , yo = 157,4o , dan zo = 157,4o

Kesebangunan Dua Segitiga

Dua segitiga dikatakan sebangun jika hanya jika memenuhi syarat berikut ini. 

(i) Perbandingan sisi-sisi yang bersesuaian senilai. 

(ii) Besar sudut-sudut yang bersesuaian sama

Jika ∆ABC dan ∆A'B'C' memenuhi syarat tersebut, maka ∆ABC dan ∆A'B'C' sebangun, dinotasikan dengan ∆ABC ∼ ∆A'B'C'. 

Jika ∆ABC dan ∆A'B'C' tidak memenuhi syarat, tersebut maka ∆ABC dan ∆A'B'C' tidak sebangun, dinotasikan dengan ∆ABC ≁ ∆A'B'C'.

Syarat Dua Segitiga Sebangun 

Untuk lebih sederhana, berdasarkan Kegiatan 2, dua segitiga dikatakan sebangun (misal: ∆ABC ∼ ∆A'B'C'), jika memenuhi salah satu kondisi berikut ini. 

1. Perbandingannya ketiga pasangan sisi yang bersesuaian sama, yaitu: 

2. Dua pasang sudut yang bersesuaian sama besar. 

Contoh: m∠A = m∠A' dan m∠B = m∠B'

3. Perbandingan dua pasang sisi yang bersesuaian sama dan sudut yang diapitnya sama besar.

Kesebangunan Khusus dalam Segitiga Siku-Siku 

Perhatikan gambar. Dengan memperhatikan bahwa ΔABC ∼ ΔDBA, ΔABC ∼ ΔDAC dan ΔDBA ∼ ΔDAC, diperoleh:

Contoh Soal

1. Perhatikan gambar di bawah ini

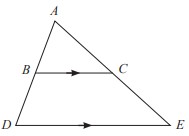
Buktikan bahwa ∆ABC ∼ ∆ADE.

Alternatif Penyelesaian: 

Pada ∆ABC dan ∆ADE dapat diketahui bahwa: 

m∠ABC = m∠ADE (karena BC//DE, dan ∠ABC sehadap 

∠ADE) m∠BAC = m∠DAC

m∠BAC = m∠DAC (karena ∠BAC dan ∠DAC berhimpit) 

Karena dua pasang sudut yang bersesuaian sama besar, jadi ∆ABC ∼ ∆ADE. (terbukti)

2. Diketahui seorang siswa dengan tinggi badan 150 cm menghadap tiang bendera pada pagi hari yang cerah. Panjang bayangan siswa adalah 2,5 m dan panjang bayangan tiang bendera adalah 6 m. Tentukan tinggi tiang bendera tersebut.

Alternatif Penyelesaian: 

Diketahui: 

Tinggi badan siswa = 150 cm

 Panjang bayangan siswa = 2,5 m = 250 cm 

Panjang bayangan tiang bendera = 6 m = 600 cm 

Misal tinggi tiang bendera = t 

Permasalahan di atas dapat dibuat model atau sketsa sebagai berikut:

Jadi, tinggi tiang bendera tersebut adalah 360 cm atau 3,6 m